- Professor: Philippe Thalmann
- Professor: Marc Vielle
- Professor: Frank Vöhringer
Learning Fourier Series and Boundary Value Problems with a view to a
variety of science and engineering problems. Learn the use of special
functions like Bessel functions and applications. Introduce the doctoral
students to general Sturm-Liouville problems and applications.
- Professor: Andrea Rinaldo
- Teacher: Cristiano Trevisin
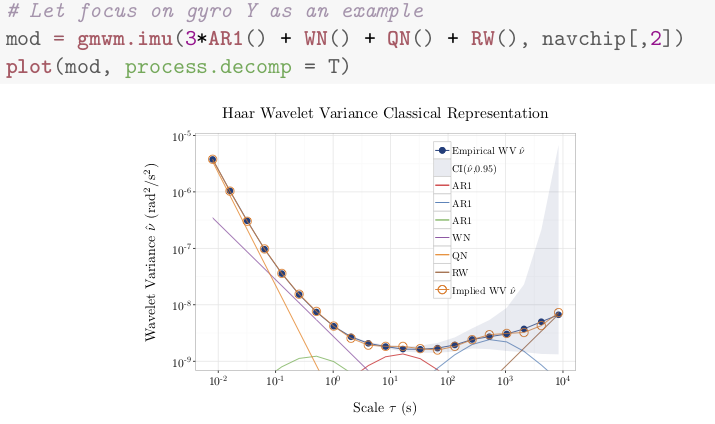
The analysis of large-scale time series is a difficult task for which most classical statistical methods (such as the maximum likelihood) are often inadequate. Indeed, these standard methods typically entail an unrealistic computational burden and are often unable to estimate complex (state-space) models. The estimation of the models used as an approximate to the stochastic behavior of various sensors (navigation sensors, oscillators, etc.) or natural phenomena (biological, chemical, etc.) is an important example of such large-scale signal processing problem. To alleviate the shortcomings of maximum likelihood methods (and other classical methods) used in this context, several new estimators have been proposed in the statistics and signal processing literature. In this course, we will discuss a new statistical method called the Generalized Method of Wavelet Moments (GMWM). This method is often the only feasible estimation approach that can be applied for complex models which are used in engineering and natural sciences. The students get familiar with its open-source distribution and practical usage that is then leveraged in the project on their own data or other use cases.
Schedule:
- Professor: Jan Skaloud
- Teacher: Mohammad Abedininajafabadi
- Professor: Alexis Berne
- Professor: Valentin Simeonov
- Teacher: Josué Etienne Gehring
- Teacher: Guillaume Anciaux
- Assistant: Emil Gallyamov