Hello I want to know the parameter in the regularization term for the linear regression and logistic regression.

And the lambda in the regularization term, 1/3:
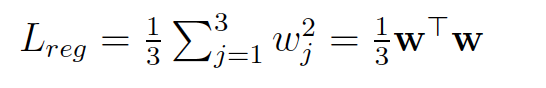
I compared the solution in other version of mock paper:

The lambda is 1/6 in the solution:

How to determine the value of lambda in the regularization term?
Moreover, when we do the polynomial feature expansion, how to determine the number of dimension after the expansion ?
For example, if x in R^2, x = [xi1, xi2] , the dimensions after expansion becomes 6, which is corresponding to [1, xi1, xi2, xi1^2, xi2^2, xi1xi2].
Thank you for your time.