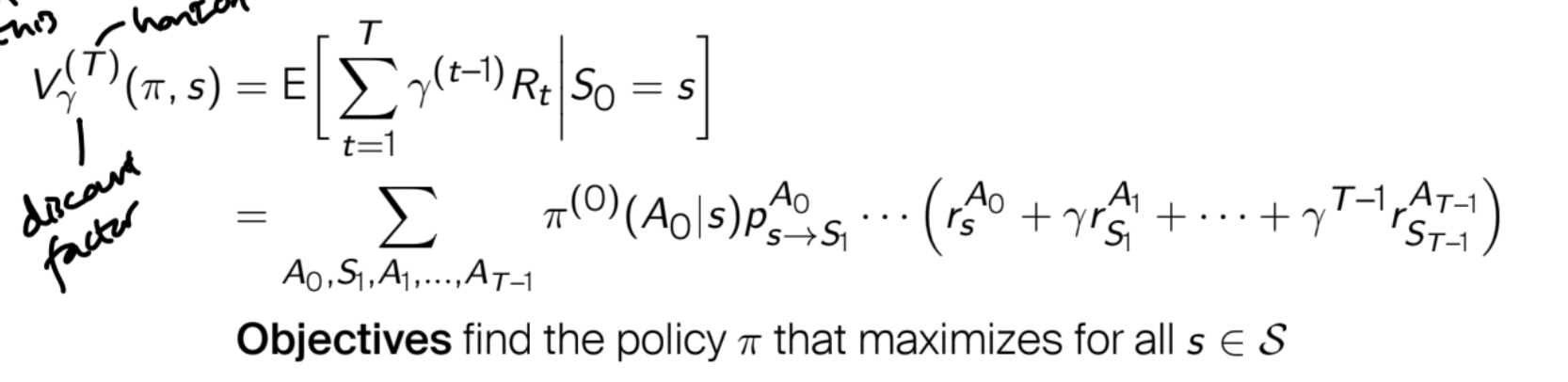Hi,
I am not a Ta so I am not completely sure, but this is my intuition.
Suppose we are working with finite state and action spaces (the countable case I think is allowed). If you want to expand the expected value defining the V value of state s computed according to the policy pi, then you can think of it as the expected value of the discounted reward over all the possible trajectories, each one weighted according to its probability.
So , how can we define the distribution over the trajectories in this case? Since you know each episode has T steps, then an episode is a choice of T states (the first one is s and is therefore fixed) and actions (which justifies the sum over all the possible choices) and the probability is given by the multiplication of the transition probability and the policy in each step (therefore I think the ... section can be filled with multiplications between the transition probabilities and the policy in later steps).
Sine we are assuming the reward function to be stochastic, we must also take care of the stochasticity coming from the reward (even if we fix the starting state, the action we take and the state in which we arrive, the reward can still be different). This is accomplished by using r, which was defined to be the expected reward when fixing (s, a, s').
Hope it helps!