Questions Forum

I just did the mock exam again for practice and ran into this exact situation. Did we ever resolve this question? 

Sorry, we have missed the initial question. 

The difference is that, Snakes model the object boundary explicitly (using a contour) where as Level-Set models the object boundary implicitly (using the zero level-set of a 2D real-valued function).

Both algorithms have specific applications. For instance, in medical imaging we have structures with fixed topology (like organs). In such cases, Snakes can work better because it can bring in the prior knowledge about the topology of the structures. 

It's also important to note that Snakes algorithm was one of the very first algorithms that introduced the idea of deforming shapes in computer vision. Level-set was introduced later addressing the limitations in Snakes. 

I also found this level-set explanation quite hard to understand, and it seems similar to the snake method. I'll try to explain what I understand, but correctness is not perfectly guaranteed. If I'm wrong somewhere TA or someone please correct me.

Both Snake and Level set are a method of segmentation with a Deformable model, meaning, given an initial curve, it deforms to fits the optimal curve.

Both methods have the target of optimizing for maximum gradient along the curve while using minimum deformation energy to keep the initial curve smooth.

The difference between the snake and level set is how they represent the curve.

Snake method represents the curve with a set of points in the image space eg. (x,y). Then it optimizes by updating these points. So, the snake represents the curve explicitly with points. Hence it cannot split into a discontinuous curve, because it is constrained to be a continuous set of points.
For example: a circle with a radius of 1, the snake would represent this curve as a set of points [(1,0), (0.95, 0.1), ..., (0,1)....] to make a circle.

Level set method represents the curve in another way. It represents in an equation. For the same circle as above, let say the level set represent it as x^2+y^2 = 1. That's why level set says to represent the curve implicitly.

Note that I want to give an intuition on how can the curve split into two. The actual representation of level set might not be this simple or not in this form.

Now consider this if you start by drawing a big circle with a radius of 5. The optimal contour is a circle radius of 1. Snake method would keep changing the set of points, recomputing the cost, and re-iterate until converge.

Level-set on the other hand, keep the same representation of the curve of  x^2+y^2 = R. But optimize by changing the R. Which can be plot as shown below. The gray plane in Z-axis is when R = 3. Imagine the gray plane move up and down to optimize and change the curve in (x,y) plane.

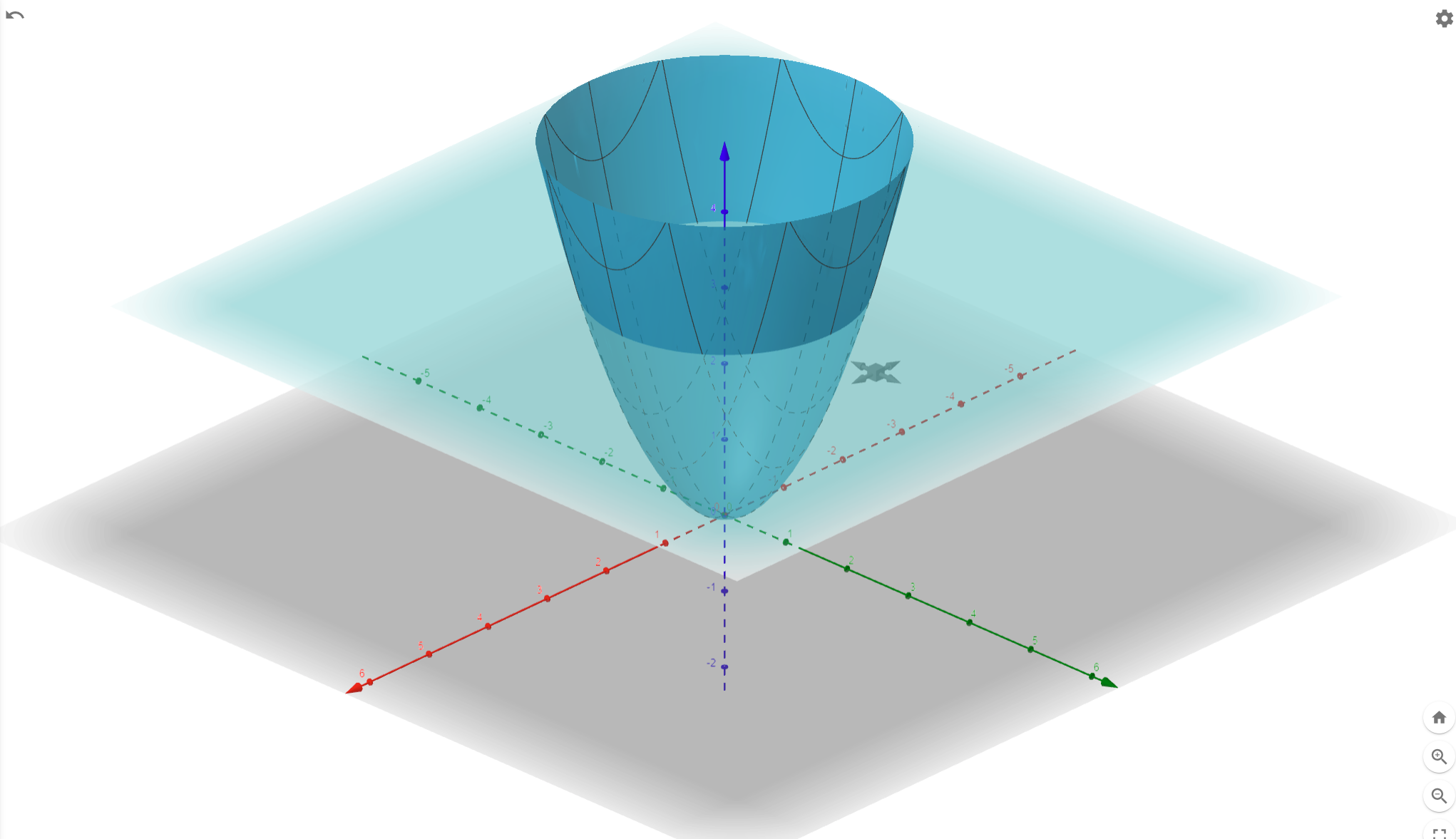
If the curve that the level-set is working on is a curve that has two humps in a 3D space as below

The level set can maintain the representation of the red "mountain" in the 3D space and optimize by moving the blue plane up and down and when projected onto the (x,y) plane, one curve can split into two as seen from the left to right.

So, the level set can maintain a single representation and consider the geometrical change in the (x,y) plane. In other word, Level set method considers topology change as the curve evolves while maintaining single representation.