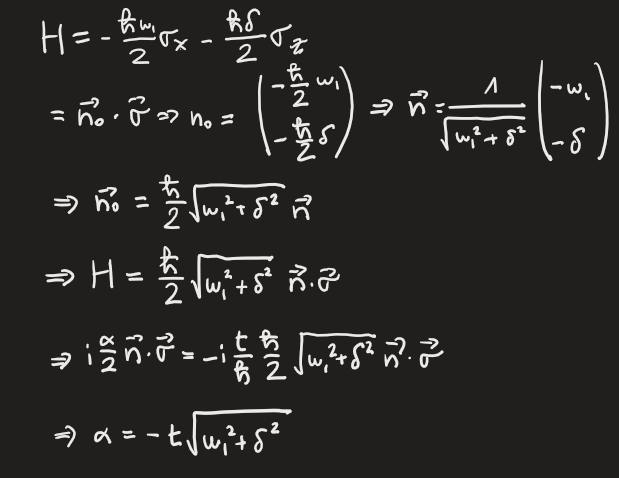HW 10, Question 1a

HW 10, Question 1a

by Benedek Hauer -
Number of replies: 5

Bonjour,

Pour le HW 10, question 1.a), j'obtiens le même résultat pour \alpha, mais je trouve que n =  \frac{1}{\sqrt{\omega_1^2+\delta^2}} \begin{bmatrix} i\omega_1 \\ 0 \\ -i\delta \end{bmatrix}.

Comme U(t,0) = exp[-i\frac{t}{2} * (sigma_x - sigma_z)], je ne suis pas sûr de comprendre où est passé le signe "-" devant le \delta ainsi que les coefficients i devant \omega_1 et \delta.

Merci d'avance et bonne journée!

Benedek Hauer
In reply to Benedek Hauer

Re: HW 10, Question 1a

by Antoine Philippe Michel Bodin -

Bonjour,

Oui il y a des erreurs qui se sont glissées dans l'énoncé / correction.

Pour rendre les choses justes, il faudrait considérer que le Hamiltonien H a aussi un signe négatif devant le premier terme en sigma_z au début de l'énoncé.

Par ailleurs, il manque également un "i" au niveau du terme de gauche dans "on rappelle la formule e^{i \frac{a}{2} n \cdot \sigma} = \ldots " (comparer avec HW8, ex1, question d pour vérifier)

Antoine
In reply to Antoine Philippe Michel Bodin

Re: HW 10, Question 1a

by Benedek Hauer -
Bonjour,

Merci pour votre réponse!

Avec H = -\frac{\hbar\omega_1}{2}\sigma_x - \frac{\hbar\delta}{2}\sigma_z et la formule corrigée e^{i\frac{\alpha}{2}n\cdot\sigma} = ..., je trouve que \alpha = -t\sqrt{\omega_1^2+\delta^2}, au lieu de t\sqrt{\omega_1^2+\delta^2} (donc de signe opposé au résultat attendu). Pour \mathbb{n}, j'obtiens \frac{1}{\sqrt{\omega_1^2+\delta^2}} \begin{bmatrix} -\omega_1 \\ -\delta \end{bmatrix}.

Cela fait du sens d'avoir \alpha positif, mais je n'arrive toujours pas à trouver mon erreur... Voici le détail de mes calculs:



Où \mathbb{n_0} correspond au vecteur \mathbb{n} non-normalisé (et \mathbb{n} est donc le vecteur normalisé).

Je vous remercie d'avance pour votre aide!

Benedek Hauer
In reply to Antoine Philippe Michel Bodin

Re: HW 10, Question 1a

by Benedek Hauer -
J'aimerais en profiter pour poser une deuxième question concernant l'exercice 1.b):

Je trouve également \frac{1}{\sqrt{2}}e^{i\frac{t\delta}{2}}(|\uparrow>+e^{-it\delta}|\downarrow>), mais je ne suis pas sûr de comprendre comment on arrive à la conclusion que \theta = \frac{\pi}{2} et que \phi = -t\delta. Ce qui me dérange, c'est le terme e^{i\frac{t\delta}{2}} devant. Est-ce qu'on le supprime car c'est une phase globale? Si oui:
1. Pourquoi peut-on le supprimer, mais on ne peut pas supprimer le \frac{1}{\sqrt{2}} qui est aussi devant l'état?
2. Quelle est la règle pour la suppression des phases globales en général?

Merci d'avance!
In reply to Benedek Hauer

Re: HW 10, Question 1a

by Nicolas Macris -
Pour la premiere question il doit s'agir d'un signe sans trop d'importance. Peut etre qu'il y a un signe global faut dans l'exponentielle de votre operateur d'evolution ? Je ne sais pas mais je ne perdaris pas trop de temps sur ca...

Pour la deuxieme question par contre la suiation est plus conceptuelle: une phase globale possede un module (valeur absolue du nb complexe) egal a 1. Donc dans la regle de Born elle n'intervient pas dans le resultat pour la probabilite. Ces phases globales sont inobservables dans les probabilites et aussi plus generalement ne sont pas des objets mesurables donc un etat (vecteur) est equivalent a tous les etats ou on multiplie par une phase globale (classe d'equivalence de vecteurs). On a donc le droit de l'eliminer dans la description de la physique. le facteur 1/sqrt 2 par contre contribue pour un facteur 1/2 dans la rege de Born: vous ne pouvez certainement pas l'eliminer dans le calcul des probabilites. De facon generale le facteur de normalisation fait que les probabilites des differents evenments possibles se somment a 1... !!! donc crucial... !!!

Remarque reliee: les phases locales (cad celles qui interviennent seulement sur une partie des termes dans une superposition et qu'on ne peut pas factoriser completement en dehors du vecteur) sont importantes et observables (par experieces d'interferences par exemple). ces phases la on ne peut certianement pas les eliminees. Quand on a un doute le mieux est de ne jamais eliminer de phase... faire les claculs justes jusqu'au bout et comme ca on ne se trompe jamais.

J'espere avoir repondu a vos questions.
N.M
In reply to Nicolas Macris

Re: HW 10, Question 1a

by Benedek Hauer -
L'explication est parfaitement claire, merci beaucoup!!

Ce qui me rend encore confus, c'est le calcul pour \theta et \phi dans l'exercice b, donc si l'on décide de ne pas éliminer le facteur e^{i\frac{t\delta}{2}}.
Alors on obtient l'équation suivante:
\cos\frac{\theta}{2}|\uparrow>+e^{i\phi}\sin\frac{\theta}{2}|\downarrow> = \frac{1}{\sqrt{2}}e^{i\frac{t\delta}{2}}(|\uparrow> + e^{-it\delta}|\downarrow>),
ce qui nous donne les équations:
\frac{1}{\sqrt{2}}e^{i\frac{t\delta}{2}} = \cos\frac{\theta}{2} (pour |\uparrow>), et
\frac{1}{\sqrt{2}}e^{-i\frac{t\delta}{2}} = e^{i\phi}\sin\frac{\theta}{2} (pour |\downarrow>).

Si l'on résoud la deuxième équation et que mes calculs sont corrects, on trouve que \theta vaut bien \frac{\pi}{2}, par contre on trouve que \phi vaut -\frac{t\delta}{2}, contrairement à -t\delta (dans le corrigé). De plus, maintenant si l'on remplace \theta dans la première équation, on trouve que
e^{i\frac{t\delta}{2}} = 1, donc \frac{t\delta}{2} = 0, ce qui impliquerait que \delta est nul et donc que \phi = 0, donc on aurait un état |\Psi> = \frac{1}{\sqrt{2}}(|\uparrow> + |\downarrow>). On n'aurait donc pas d'oscillements et l'état serait l'état initial du système.

Donc en gardant le facteur e^{i\frac{t\delta}{2}}, on obtient un résultat différent de si on le supprime comme dans le corrigé. Ou ai-je fait une faute de calcul quelque part, ou ma démarche serait-elle incorrecte?

Merci beaucoup pour votre temps et aide!

Benedek Hauer