Hi,
I want to ask a question about the equation on P13 of Lecture Shape from Texture as following shown:
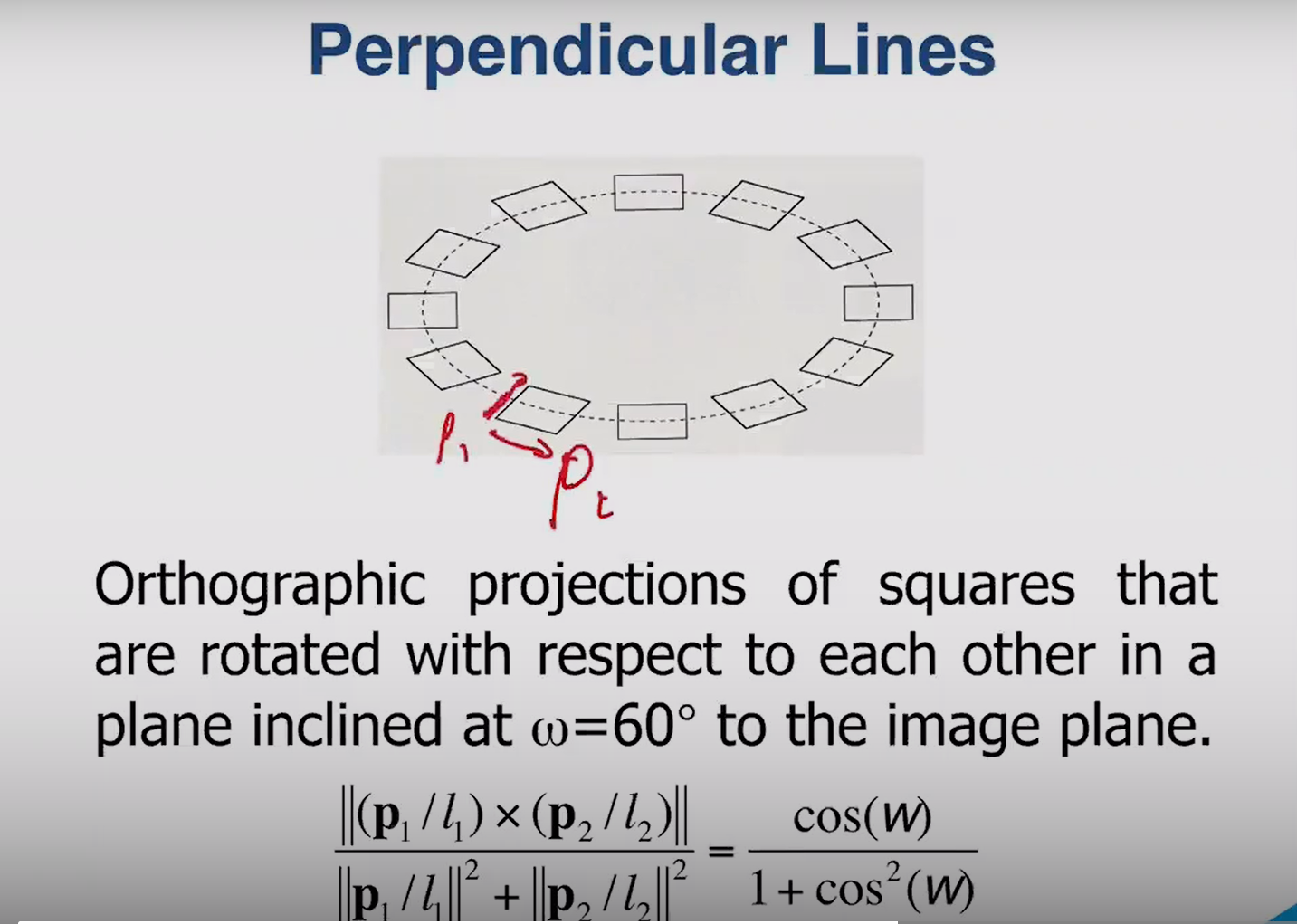
It seems that the left side is a scaled value of sin(θ) (θ is the angle between p1 and p2). And the right side is a constant for the plane with ω=60° to the image plane. It indicates that for all perpendicular lines in this plane, the angle between p1 and p2 will be the same but it is not the case.
Is there anything I mis-understand?
Thanks in advance!